解直角三角形 巩固训练
【巩固训练】
1、选择题
1.在△ABC中，∠C＝90°，
，则cotB＝．
A．
B．
C．
D．
2．在Rt△ABC中，∠C＝90°，∠B＝35°，AB＝7，则BC的长为．
A．7sin35° B．
C．7cosplay35° D．7tan35°
3．河堤、横断面如图所示，堤高BC＝5米，迎水坡AB的坡比是1:
，则AC的长是．
A．
米 B．10米 C．15米 D．
米
4．如图所示，正方形ABCD中，对角线AC、BD交于点O，点M、N分别为OB、OC的中点，则cosplay∠OMN的值为．
A．
B．
C．
D．1
第3题 第4题 第5题
5．如图所示，某游乐场一山顶滑梯的高为h，滑梯的坡角为α，那样滑梯长
为
A． B．
C． D．
6．如图所示，在△ABC中，∠C＝90°，AC＝16 cm，AB的垂直平分线MN交AC于D，连接BD，
若
，则BD的长是．
A．4 cm B．6 cm C．8 cm D．10 cm
7．如图所示，一艘轮船由海平面上A地出发向南偏西40°的方向行驶40海里到达B地，再由B地向北偏西
的方向行驶40海里到达C地，则A、C两地相距．
A．30海里 B．40海里 C．50海里 D．60海里
第6题 第7题 第8题
8．如图所示，为了测量河的宽度，王芳同学在河岸边相距200m的M和N两点分别测定对岸一棵树P的地方，P在M的正北方向，在Ⅳ的北偏西30°的方向，则河的宽度是．
A．
m B．m C．m D．100m
2、填空题
9．如图所示，在Rt△ABC中，∠C＝90°，AM是BC边上的中线，sin∠CAM＝，则tan∠B的值为______．
10．如图所示，等边三角形ABC中，D、E分别为AB、BC边上的点，AD＝BE，AE与CD交于点F，AG⊥CD于点G，则的值为________．
第9题 第10题 第11题
11．如图所示，一艘海轮坐落于灯塔P的东北方向，距离灯塔
海里的A处，它沿正南方向航行一段时间后，到达坐落于灯塔P的南偏东30°方向上的B处，则海轮行驶的路程AB为________海里．
12．如图所示，直角梯形ABCD中，AB⊥BC，AD∥BC，BC＞AD，AD＝2，AB＝4，点E在AB上，将△CBE沿CE翻折，使B点与D点重合，则∠BCE的正切值是________．
13．如图所示．线段AB、DC分别表示甲、乙两座建筑物的高．AB⊥BC，DC⊥BC，两建筑物间距离BC＝30米，若甲建筑物高AB＝28米，在A点测得D点的仰角α＝45°，则乙建筑物高DC＝____米．
第12题 第13题 第14题
14.在一次夏令营活动中，小明同学从营地A出发，要到A地的北偏东60°方向的C处，他先沿正东方向走了200m到达B地，再沿北偏东30°方向走，恰能到达目的地C，那样，由此可知B、C两地相距________m．
3、解答卷
15．如图所示，某校综合实践活动小组的同学欲测量公园内一棵树DE的高度，他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°，朝着这棵树的方向走到台阶下的点C处，测得树顶端D的仰角为60°．已知A点的高度AB为2米，台阶AC的坡度为1:，且B、C、E三点在同一条直线上．请依据以上条件求出树DE的高度．
16. 如图所示，某校数学兴趣小组的同学欲测量一座垂直于地面的古塔BD的高度，他们先在A处测得古塔顶端点D的仰角为45°，再沿着BA的方向后退20m至C处，测得古塔顶端点D的仰角为30°．求该古塔BD的高度．
17．如图所示是某品牌太阳能热水器的实物图和横断面示意图，已知真空集热管AB与支架CD所在直线相交于水箱横断面⊙O的圆心，支架CD与水平面AE垂直，AB＝150厘米，∠BAC＝30°，另一根辅助支架DE＝76厘米，∠CED＝60°．
求垂直支架CD的长度．
求水箱半径OD的长度．
【答案与分析】
1、选择题
1.【答案】A；
【分析】如图，sin A＝
，设BC＝4x．则AB＝5x．
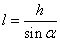
依据勾股定理可得AC＝
，∴．
2.【答案】C；
【分析】在Rt△ABC中，
．∴BC＝ABcosplayB＝7cosplay 35°．
3.【答案】A；
【分析】由
知，
．
4.【答案】B；
【分析】由题意知MN∥BC，∠OMN＝∠OBC＝45°，∴
．
5.【答案】A；
【分析】由概念
，∴.
6.【答案】D；
【分析】∵MN是AB的中垂线, ∴BD＝AD．又
，
设DC＝3k，则BD＝5k，∴AD＝5k，AC＝8k．∴8k＝16，k＝2，BD＝5×2＝10．
7.【答案】B；
【分析】 连接AC，∵AB＝BC＝40海里，∠ABC＝40°+20°＝60°，
∴ △ABC为等边三角形，∴ AC＝AB＝40海里．
8.【答案】A
【分析】依题意PM⊥MN，∠MPN＝∠N＝30°，tan30°
，
．
2、填空题
9．【答案】
；
【分析】在Rt△ACM中，sin∠CAM＝，设CM＝3k，则AM＝5k，AC＝4k．
又∵AM是BC边上的中线，∴BM＝3k，∴tan∠B＝
．
10．【答案】
【分析】由已知条件可证△ACE≌△ACB．从而得出∠CAE＝∠BCD．
∴∠AFG＝∠CAE+∠ACD＝∠BCD+∠ACD＝60°，在Rt△AFG中，
．
11．【答案】
；
【分析】在Rt△APC中，PC＝AC＝AP·sin∠APC＝
．
在Rt△BPC中，∠BPC＝90°-30°＝60°，BC＝PC·tan∠BPC＝，
所以AB＝AC+BC＝．
12．【答案】
【分析】如图，连接BD，作DF⊥BC于点F，则CE⊥BD，∠BCE＝∠BDF，BF＝AD＝2，DF＝AB＝4，所以．
13．【答案】58；
【分析】∵α＝45°，∴DE＝AE＝BC＝30，EC＝AB＝28，DE＝DE+EC＝58
14．【答案】200；
【分析】由已知∠BAC＝∠C＝30°，所以BC＝AB＝200.
3、解答卷
15.【答案与分析】
过点A作AF⊥DE于F，则四边形ABEF为矩形，
∴AF＝BE，EF＝AB＝2．设DE＝x，
在Rt△CDE中，
．
在Rt△ABC中，∵，AB＝2，∴
．
在Rt△AFD中，DF＝DE-EF＝x-2．
∴
∵AF＝BE＝BC+CE．
∴，解得
．
答：树DE的高度为6米．
16.【答案与分析】
依据题意可知：∠BAD＝45°，∠BCD＝30°，AC＝20m．
在Rt△ABD中，由∠BAD＝∠BDA＝45°，得AB＝BD．
在Rt△BDC中，由tan∠BCD＝，得
．
又∵BC-AB＝AC．∴
，∴BD＝≈27.3．
答：该古塔的高度约为27.3m．
17.【答案与分析】
在Rt△DCE中，∠CED＝60°，DE＝76，
∵sin∠CED＝
，∴DC＝DE×sin∠CED＝
答：垂直支架CD的长度为厘米．
设水箱半径OD＝x厘米，则OC＝
厘米，AO＝厘米，
∵Rt△OAC中，∠BAC＝30°
∴AO＝2×OC，即150+x＝
，
解得：
≈18.52≈18.5
答：水箱半径OD的长度约为18.5厘米．
